1. 无源滤波
无源滤波主要是使用无源的器件，比如电阻，电容，电感组成的滤波器，有低通滤波，高通滤波，LC滤波以及π型滤波。无论是哪种滤波形式，其目的都是让有用的信号通过，无用的信号衰减。
2. RC滤波器RC滤波器由电阻和电容两个器件组成，根据R和C位置的不同，分为低通滤波和高通滤波。
3. 低通滤波器
低通滤波器的电路如图所示。低通滤波器顾名思义，当信号频率比滤波器的截止频率低时，可以正常通过，当信号频率比滤波器的截止频率高时，信号会呈现衰减的形式。有两个角度可以解释低通滤波器的工作原理。
第一个角度是基于电容的工作原理——隔直通交。假设输入信号为直流时，此时的电容对直流信号的阻抗非常大，则信号会经过电阻到达输出端。若输入信号为高频的交流信号时，此时的C1可以看成是短路，则滤波电路等效为下面的形式：
此时在接收端接收到的信号，会因为有部分高频信号通过电容直接到地，因此得到的输出信号比输入信号要弱，也就起到了滤波的作用。
第二个角度是基于电路分析的角度，通过传递函数来分析低通滤波的原理。
从传递函数的表达式可以看出，传递函数和输入信号频率之间存在相关性。为了更加清楚的分析出输入信号与滤波器截止频率之间的关系，令：
则传递函数的表达式为：
根据复数的性质可知，传递函数的模代表了输出信号与输入信号之间大小的关系，传递函数的相位代表了输出信号与输入信号之间的相位关系。这里只研究输出信号的特性。因此H(S)的的幅值为：
当滤波器的RC参数设定以后，截止频率fo为定制。当输入信号频率远小于fo时，此时HS的幅值接近为1，即输入信号不衰减到达输出。当输入信号源大于fo时，此时Hs幅值将小于1，则输出信号相对输入信号呈现衰减。当f和fo相等时，此时输出信号的幅值是输入信号的0.707107倍。此时信号频率的大小刚好就是低通滤波的带宽。
上面都是基于理论的分析，使用TINA软件对低通滤波器进行仿真。
根据RC的参数，可以计算出滤波器的截止频率为15.9Hz。根据仿真幅值曲线可以看出，截止频率以前的输入信号从无衰减到慢慢增加到-3dB，当超过截止频率后，信号将以-20dB/dec的斜率开始下降。
4. 高通滤波器
高通滤波器和低通滤波器的器件一样，仅仅是位置发生了变化。如下图所示。
高通滤波器的分析和推导方式和低通滤波器几乎一致。这里不再进行推导。在高通滤波器中，还有两种变形的RC电路使用比较广泛。如下图所示。
这两种变形的形式是基于电容“隔直通交”的特性。根据电容的阻抗公式可知：
复制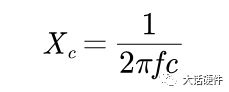当电容的容值固定时，通过电容信号的频率越高，电容呈现出来的阻抗越小，也就是高频信号越容易通过。即呈现出高通的特性。下面分别对不同形式的高通滤波器进行仿真。
4.1 无源高通滤波器
从上面的仿真的结果可以看出，高于截止频率以上的信号，可以无衰减的通过，低于截止频率的信号呈现衰减的形式。
4.2 有源高低通滤波器
有源高通和低通，会把前面的低通和高通结合起来一起进行仿真，原理图如下所示
幅频特性曲线如下所示
根据仿真可知，高通截止频率为15.9Hz，低通的截止频率为15.9K。红色框中的RC是高通滤波，绿色框中是低通滤波。
以上即为有源高通滤波器的原理和仿真。
在计算滤波器的截止频率时可以使用下面的公式：
5. 总结
滤波器在电路设计中用的比较广泛，简单就两个器件的参数计算，复杂的可以设计成不同的音频滤波器，无论是哪种用法，抓住滤波器的本质——有用的信息留下，没用的信息剔除掉。RC滤波器相对简单一点，复杂的是LC滤波器，π型滤波器以及T型滤波器，后面继续更新。
文章中使用的画图软件是嘉立创在线的EDA软件，TI的仿真TiNA，公式编辑使用的是AxMath。
