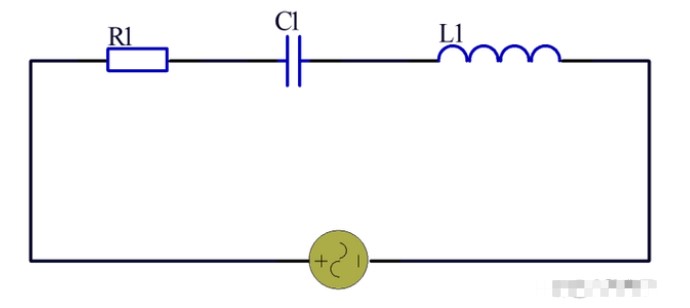
RLC串联谐振电路的特点-rlc串联谐振电路的谐振特性

RLC串联谐振电路

上图的阻抗为：

Z=R+LS+1/SC

Z=R+Ljω+1/jωC

Z=R+j(ωL-1/ωC)

阻抗的模为：

|Z|=√(R^2+(ωL-1/ωC)^2 )

相角为：

θ=arctan((ωL-1/ωC)/R)

当ωL-1/ωC=0，即ω=1/√LC 时，θ=0°，|Z|=R，电压与电流相位相同，电路发生谐振。

也就是说RLC串联电路谐振的条件是

ω=ω0=1/√LC

当输入信号的频率与谐振频率相同时，电路发生谐振。用频率表示的谐振条件为

f=f0=1/(2π√LC)

谐振时，感抗和容抗在量值上相等，这个值称为谐振电路的特征阻抗，用ρ表示

ρ=ω0*L=1/(ω0*C)=√(L/C)

此时电流达到最大值,且与电压源电压同相。此时电阻、电感和电容上的电压分别为：

UR=RI=US

UL=j*ω0*L*I=j *(ω0 L)/R *US=j*Q*US

UL=-j *1/(ω0*C)*I=-j*1/(ω0*R*C)*US=-j*Q*US

振电路的特性阻抗ρ与电路中电阻R的比值大小来表征谐振电路的性能,也可以说是电感电压和电容电压的倍数，这个值称为电路的品质因数,用字母Q表示。即:

Q=ρ/R=(ω0* L)/R=1/(ω0*R*C)=（1/R） * √(L/C)

RLC串联谐振曲线

串联谐振电路对不同频率的信号有不同的响应,对谐振信号最突出(表现为电流最大),而对远离谐振频率的信号加以抑制(电流小)。这种对不同输入信号的选择能力称为”选择性”。

Q越大,谐振曲线越尖。当稍微偏离谐振点时,曲线就急剧下降,电路对非谐振频率下的电流具有较强的抑制能力(抑非能力),所以选择性好。

谐振曲线上,电流I不小于谐振电流Io的0.707所对应的频率范围称为电路的通频带。

通频带越窄,电流的选择性越好。

当ω<ω0时, XL

当ω>ω0时, XL >XC,电路呈电感性。

电抗的频率特性