一、什么是Fisher判别
Fisher线性判别给模式识别问题提供了一个新思路，与Bayes决策以及其他的决策方法直接处理高维问题不同，Fisher线性判别是将d维数据投影到1维空间进行分类。因此，使用Fisher线性判别进行分类就可以归结为寻找最佳投影方向的问题，在这个最佳投影方向上，样本的投影能够分开得最好。
如图，将二维平面中的数据投影到一条直线上之后，分类问题就简单很多，我们只需要找到一个点作为分类边界即可。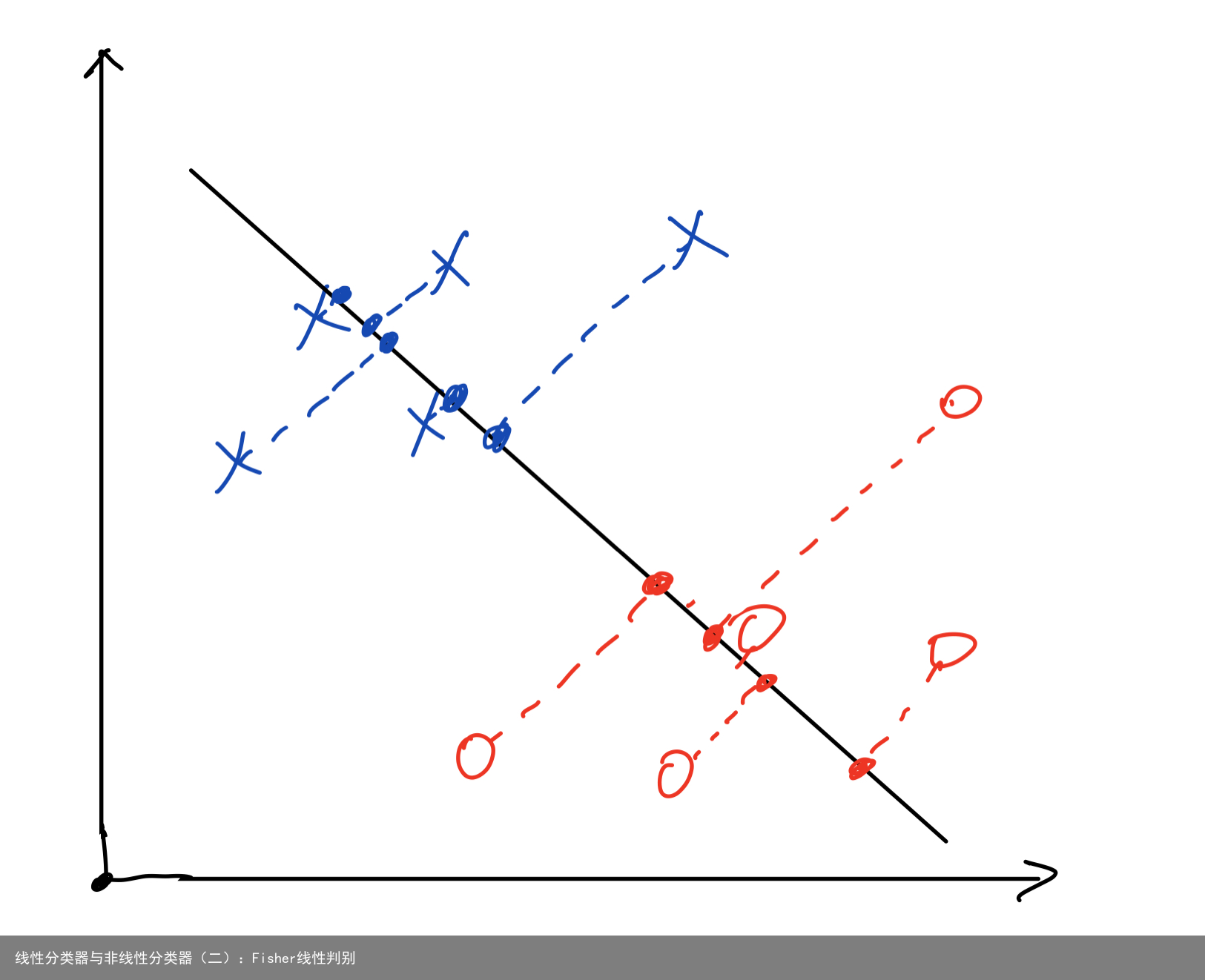
Fisher线性判别要解决的基本问题就是确定最佳投影方向。要确定最佳的投影方向，首先得计算出类内离散度和各类样本的均值，然后通过相应公式即可计算出最佳投影距离。最后确定一维空间的分类阈值，从而对样本进行分类。分类阈值的确定有三种方法——均值中点法、类样本数加权法和先验概率加权法。 具体Matlab实现如下： （1）导入数据，获取相关信息，并计算各类样本的均值。flag变量用于选择分类阈值的确定方法。
clear load(2-Class Problem.mat) flag=3;% 1:均值中点法。2:类样本数加权法。3:先验概率加权法 tic % 获取数据集信息 [d1,n1]=size(Training_class1); [d2,n2]=size(Training_class2); test_num=size(Testing,2); % 各类样本均值 m1=sum(Training_class1,2)/n1; m2=sum(Training_class2,2)/n2;（2）计算类内离散度，计算最佳投影方向并将数据投影到一维空间
% 计算类内离散度 s1=(Training_class1-m1)*(Training_class1-m1); s2=(Training_class2-m2)*(Training_class2-m2); % 最佳投影方向 w=(s1+s2)\(m1-m2); % 将数据投影到一维Y空间 y1=w*Training_class1; m1_=sum(y1)/n1; y2=w*Training_class2; m2_=sum(y2)/n2; y=w*Testing;（3）确定分类阈值并进行分类 a.使用均值中点法：
% 预测 if flag==1 % 使用均值中点法确定分类阈值 y01=(m1_+m2_)/2; predict=0; for i=1:test_num if y(i)>y01 predict(i)=1; else predict(i)=2; end end acc=sum(predict==Label_Testing)/test_num; fprintf(使用均值中点法，准确度为：%.2f%%\n,acc*100);b.使用类样本数加权法：
elseif flag==2 % 使用类样本数加权法 y02=(n1*m1_+n2*m2_)/(n1+n2); predict=0; for i=1:test_num if y(i)>y02 predict(i)=1; else predict(i)=2; end end acc=sum(predict==Label_Testing)/test_num; fprintf(使用类样本数加权法，准确度为：%.2f%%\n,acc*100);c.使用先验概率加权法：
else % 使用先验概率加权法 pw1=n1/(n1+n2); pw2=n2/(n1+n2); y03=(m1_+m2_)/2+(log(pw1)-log(pw2))/(n1+n2-2); predict=0; for i=1:test_num if y(i)>y03 predict(i)=1; else predict(i)=2; end end acc=sum(predict==Label_Testing)/test_num; fprintf(使用先验概率加权法，准确度为：%.2f%%\n,acc*100); end toc完整代码如下：
clear load(2-Class Problem.mat) flag=3;% 1:均值中点法。2:类样本数加权法。3:先验概率加权法 tic % 获取数据集信息 [d1,n1]=size(Training_class1); [d2,n2]=size(Training_class2); test_num=size(Testing,2); % 各类样本均值 m1=sum(Training_class1,2)/n1; m2=sum(Training_class2,2)/n2; % 计算类内离散度 s1=(Training_class1-m1)*(Training_class1-m1); s2=(Training_class2-m2)*(Training_class2-m2); % 最佳投影方向 w=(s1+s2)\(m1-m2); % 将数据投影到一维Y空间 y1=w*Training_class1; m1_=sum(y1)/n1; y2=w*Training_class2; m2_=sum(y2)/n2; y=w*Testing; % 预测 if flag==1 % 使用均值中点法确定分类阈值 y01=(m1_+m2_)/2; predict=0; for i=1:test_num if y(i)>y01 predict(i)=1; else predict(i)=2; end end acc=sum(predict==Label_Testing)/test_num; fprintf(使用均值中点法，准确度为：%.2f%%\n,acc*100); elseif flag==2 % 使用类样本数加权法 y02=(n1*m1_+n2*m2_)/(n1+n2); predict=0; for i=1:test_num if y(i)>y02 predict(i)=1; else predict(i)=2; end end acc=sum(predict==Label_Testing)/test_num; fprintf(使用类样本数加权法，准确度为：%.2f%%\n,acc*100); else % 使用先验概率加权法 pw1=n1/(n1+n2); pw2=n2/(n1+n2); y03=(m1_+m2_)/2+(log(pw1)-log(pw2))/(n1+n2-2); predict=0; for i=1:test_num if y(i)>y03 predict(i)=1; else predict(i)=2; end end acc=sum(predict==Label_Testing)/test_num; fprintf(使用先验概率加权法，准确度为：%.2f%%\n,acc*100); end toc<
运行结果分析:Fisher线性判别处理二分类问题时，运行时长都在0.01s以内，而且三种分类阈值确定方法均可达到100%的分类正确率。
Fisher线性判别从另一个思路出发，将高维度问题转换到了一维分类问题，大大降低了程序的运行耗时，提高程序运行效率。这种方式对于我们日后对高维数问题的降维处理提供了思路。
