我们最终的目的，就是要创造一个机器，这个机器可以通过对真实世界的学习，从而可以独立地完成所有人类可以完成甚至是不能完成的任务。其实这个机器已经存在，那就是人类的大脑。我们为何不从人类的大脑开始研究，通过模仿大脑的学习过程，实现真正的人工智能。
这个概念很早就被科学家们提出来了，这也就是我们本篇文章要讨论的内容。在讨论神经网络之前，我们可以先从神经元开始。大脑强大的神经网络就是由一个个神经元组成的，如图所示：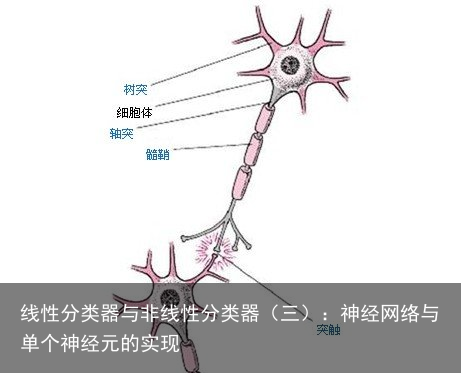
大脑进行学习行为的基础就是这些个神经元。外界信号进入大脑后，又传播到大脑的各个区域，这些区域各司其职，进行信号的处理。最终将结果与大脑之前存储的记忆进行对比，若有不一致的地方，大脑就会自行改变神经网络的结构以进行纠正，这便是大脑不断学习的过程。大脑记忆的内容，便是人类不断实践积累的经验。我们也可以仿照此过程实现我们的人工智能机器。首先，我们将信号送入我们创建的神经网络，然后将输出与我们已知的样本数据进行对比，然后不断纠正神经网络的结构，直到网络的输入与样本的偏差在容忍范围之内。上述过程，便是bp神经网络的基本原理。
如图，我们可以模仿神经元，将其抽象为数学函数，如图所示：
图中的单个神经元，可以获取上层的多个神经元的输入x1、x2、x3，每个输入都有各自对应的权值wi，此外，神经元还有一个偏置b，这里为了方便理解，可以举个例子：加入今天我们想判断老板中午会不会吃鸡排饭，现在我们有3个判断依据，分别是鸡排饭的美味程度、鸡排饭餐馆的远近以及作为员工的你爱不爱吃鸡排饭。显然，每个依据在老板心中都有自己的占比，假设鸡排饭足够美味，以至于老板不惜开一个小时车去吃，那么老板就优先考虑美味程度；第三个因素一般对老板没有什么影响，所以第三个因素在老板心中的占比几乎为0，这个概念就是权值的概念，偏置就好理解了，如果神经网络的输出与样本恒定有个差值，那么加一个偏置，可以让输出整体进行数值上的偏移。这就是权值w和偏置b的概念。
最终，输入的数据通过神经元的处理得到结果。然后将结果与已有的样本数据进行对比，调整每个输入对应的权值，以降低输出与样本的偏差，达到分类的效果。所用数据集结构如下：
数据维度为190.
下面是matlab具体实现：
编程思路：使用matlab工具箱创建单层神经元解决简单的二分类问题。因为实验所用的二分类数据线性可分，所以可以尝试使用单个感知器神经元进行分类。
相关代码如下：
（1）导入数据集并作相应处理
（2）数据归一化并设计网络
% 数据归一化 [Training,ps]=mapminmax(Training,0,1); Testing=mapminmax(apply,Testing,ps); pr=[0,1].*ones(190,2); % 定义一个神经元，190个输入，1个输出 net=newp(pr,1); % 网络初始化 net=init(net);（3）训练网络并预测
% 训练网络 net=train(net,Training,Label_Training); % 对测试数据进行分类 predict=sim(net,Testing); acc=sum(predict==Label_Testing)/n ; toc disp([准确度是： num2str(acc)])完整代码如下：
clear load(2-Class Problem.mat) tic % 制作训练数据标签 n1=size(Training_class1,2); n2=size(Training_class2,2); Label_Training1=zeros(1,n1); Label_Training2=ones(1,n2); Label_Training=[Label_Training1,Label_Training2]; % 合并训练数据 Training=[Training_class1,Training_class2]; % 处理数据标签，使其范围在0-1之间 n=size(Testing,2); Label_Testing=Label_Testing-1; % 数据归一化 [Training,ps]=mapminmax(Training,0,1); Testing=mapminmax(apply,Testing,ps); pr=[0,1].*ones(190,2); % 定义一个神经元，190个输入，1个输出 net=newp(pr,1); % 网络初始化 net=init(net); % 训练网络 net=train(net,Training,Label_Training); % 对测试数据进行分类 predict=sim(net,Testing); acc=sum(predict==Label_Testing)/n ; toc disp([准确度是： num2str(acc)])程序结果分析：
训练进行了5次，最终达到100%的正确率，耗时2.6s。
本篇文章实现了单个神经元，这个是接下来要讨论的bp神经网络的基础，不足的是，单个神经元的输出本质上是线性函数，只能适用于线性可分的情况，要应用在实际情况中，还是需要使用更加复杂的神经网络。虽然单个神经元的输出是线性的，但是由多个神经元组成的神经网络可以用于非线性输入输出关系的分类，理论上来说，网络足够复杂以及足够学习样本数量的情况下，我们可以实现所有的分类任务。下篇文章，我们将讨论bp神经网络的实现。
