模式识别之数据降维（二）：使用遗传算法选择的特征进行分类测试

  上一篇文章，我们介绍了如何使用遗传算法进行特征选择，并且已经选择出最优的40个特征，这篇文章，我们就来看看，这40个特征能否达到良好的分类效果。

一、二分类测试

数据集结构如图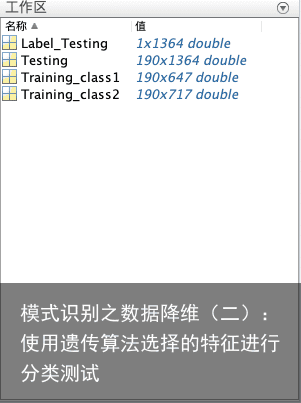： 同时加载已经选择好的40个特征索引（图中红框部分） 测试算法使用最小错误bayes估计算法，概率密度估计方式为参数估计，这个算法在之前的文章中讲过，大家可以点击链接进行查阅。

下面我们进行测试：

clear load(2-Class Problem.mat); load(feature_selected_GA); tic %获取训练数量 n1=size(Training_class1,2); n2=size(Training_class2,2); % 先验概率 pw1=n1/(n1+n2); pw2=n2/(n1+n2); dim=size(Training_class1,1);%维数 Training_data1=Training_class1(feature_selected,:); Training_data2=Training_class2(feature_selected,:); Testing_data=Testing(feature_selected,:); %参数估计 [miu1,sigma1]=ParamerEstimation(Training_data1); [miu2,sigma2]=ParamerEstimation(Training_data2); %预测结果 predict_label=0; test_num=size(Testing,2);%获取测试数据数量 for i=1:test_num x=Testing_data(:,i); pxw1=gaussian(miu1,sigma1,x); pxw2=gaussian(miu2,sigma2,x); if pw1*pxw1>pw2*pxw2 predict_label(i)=1; else predict_label(i)=2; end end % 计算精度 acc=sum(predict_label==Label_Testing)/test_num; fprintf(正确率是%.2f%%\n,acc*100); toc

程序运行结果： 因为只用了40个特征，所以程序运行速度大大提升，并且可以实现100%分类。

二、多分类测试

数据集结构如下： 并导入已选择的40个特征索引： 测试使用算法同样为最小错误bayes估计算法，概率密度估计使用参数估计方法，该算法同样已经实现过了，可以根据链接进行查阅。

clear warning off; % 读取多分类数据集和选择的40个最优特征 load(Mult-class Problem.mat); load(feature_selected_GA); tic % 去除无关的特征，只保留40个已选择特征 Training_data=Training_data(feature_selected,:); Testing_data=Testing_data(feature_selected,:); class_nums=Label_training(end);% 获取类别数 test_nums=size(Testing_data,2);% 获取测试集大小 train_nums=size(Training_data,2); % 获取训练集大小 Training_temp=0; predict=0; for class=1:class_nums [miu(:,class),sigma(:,:,class)]=ParamerEstimation(Training_data(:,Label_training==class)); num=size(Training_data(:,Label_training==class),2); pw(class)=num/train_nums;% 计算先验概率 end for i=1:test_nums for class=1:class_nums % 计算类的条件概率密度 pxw(class)=gaussian(miu(:,class),sigma(:,:,class),Testing_data(:,i)); % 计算判别式 g_x(class)=log(pw(class))+log(pxw(class)); end [~,argmax]=max(g_x); predict(i)=argmax; if mod(i,100) == 0 acc=sum(predict==Label_testing(1:i))/(i); disp([预测数据号： num2str(i)]) disp([准确度是： num2str(acc)]) end end acc=sum(predict==Label_testing)/(test_nums); toc disp([总准确度是： num2str(acc)])

程序运行部分结果：   相比使用全部的特征进行分类，运行时间减少了大约40倍！（使用全部特征进行分类时长为340s左右，进行降维后仅用了8s），但是正确率有下降，这也在预料之中，因为在进行数据降维时难免会丢失一些信息。

三、总结

  不难看出，使用特征选择进行降维后，程序依然能保证正确率，同时大大降低运行时长，总体来说，程序运行效率得到了提升。但是我们依然能够发现一些问题，在进行特征选择后，由于大量的特征未被选择，因此丢失了数据携带的部分信息，所以分类的正确率会受到影响。