之前的文章中，我们提到，数据降维大体可以分为两类：特征选择和特征提取。前面的四篇文章我们介绍了特征选择的方法，从这篇文章开始，我将为大家介绍特征提取的方法。由于特征选择会丢弃大量特征，这些特征虽然对分类影响不大，但是毕竟会包含一些信息，所以丢弃这些特征意味着多少会丢弃较多的对分类有用的信息，所以我们在实际分类任务中往往不会使用特征选择进行特征降维。下面介绍的特征提取的方法，使通过将数据进行一定的变换，从高维数据变换到低维度数据，以达到降维的效果，同时不会丢弃大量信息。如图所示，我们可以将二维平面中的点投影到一条直线上，关于这个，我们之前已经遇见过了，即fisher线性判别法。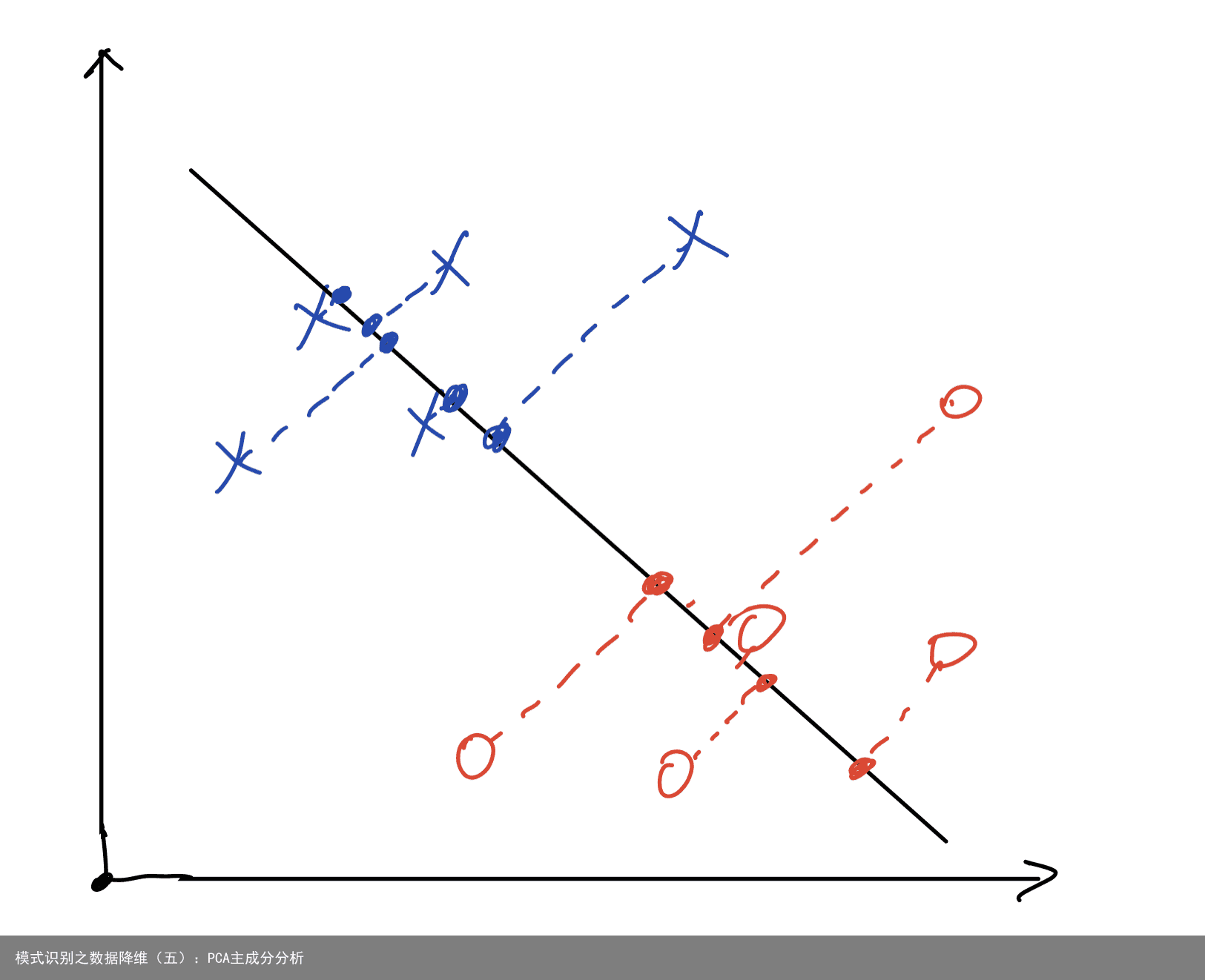
这和特征提取的基本原理类似，不同的是，fisher线性判别会把高维数据投影到一条直线上，而特征提取是将高维数据进行一定变换，不一定是投影法，也不一定是投影到一条直线（高维投影到低维即可）。可以这么讲，fisehr线性判别法一定程度上属于特征提取。
PCA（Principal Component Analysis）即主成分分析。它的基本原理就是将数据维度映射到低维，假设我们将n维数据映射到了m维，映射后的数据有以下特点：从第1维到第m维，数据的方差依次递减。我们知道，方差代表数据的离散程度，方差越大，说明数据越分散，数据越分散，我们就越容易找到不同类别之间的分类界限。映射完成后，我们从第一维开始，选择所需要的k维数据（k< m)进行最终的分类，以实现降维（m维到k维），这样，选择的k维数据就是数据方差最大的k维数据，也就是对分类最有帮助的k维数据。具体的PCA数学原理推导大家可以自行百度，本篇文章具体介绍PCA的编程实现部分。
我们首先需要将数据整体“搬移”到坐标原点，如图：
按公式计算协方差矩阵，然后求出该矩阵的特征值和对应的特征向量。在用Matlab实现的时候，我们直接可以用相应函数进行特征值和特征向量的求解。
3 选择特征向量并保存首先，对特征向量按特征值的大小进行排序，然后根据我们要求的信息保留量确定需要选择多少个特征向量，我们具体按照如下方式确定选择特征向量的个数：选择的前k个特征向量值的累加和与所有特征值的和之比等于保留的信息百分比。选择好特征向量之后，将特征向量保存。在之后的数据降维时，我们将使用这些特征向量构建新的样本空间，新的样本空间就是降维后的新样本。
三、Matlab编程实现按照PCA的步骤依次去均值化、计算去均值化后数据的协方差阵、计算协方差阵的特征值和特征向量，然后对特征向量进行排序，最后取前K个主成分特征向量，完成主成分的提取，实现维数约减。 （1）读取数据集并合并。因为PCA分析并不需要知道数据的标签，所以可以用所有的数据进行PCA分析。
%PCA主成分分析 clear load(2-Class Problem.mat); load(Mult-class Problem.mat); tic % 因为PCA分析时不需要标签信息，所以我们可以使用所有数据进行PCA，提高分析性能 datas=[Training_class1,Training_class2,Testing,Training_data,Testing_data];%将所有数据整合到一起 [d,n]=size(datas);%获取数据大小，d为维度，n为数据数量（2）去均值化，计算协方差矩阵以及协方差阵的特征值和特征向量
% 去均值化 datas_mean=mean(datas,2); datas=datas-datas_mean; % 计算协方差阵 c=datas*datas/n; % 计算特征值和特征向量 [u,lamda]=eig(c); lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量（3）对特征向量按特征值进行排序
%将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列 lamda_u=[lamda;u]; lamda_u=lamda_u; % 对特征向量按lamda大小进行降序排列，并确定K，阈值选0.9 thr=0.9; lamda_u=sortrows(lamda_u,1,descend);%对特征向量按lamda大小进行降序排列 lamda=lamda_u(:,1);%分离特征值 u=lamda_u(:,2:end);%分离特征向量（4）确定阈值并进行特征提取，将含有主成分信息的特征值保存下来
%确定K值 for i=1:d res=sum(lamda(1:i))/sum(lamda); if res>thr k=i; break end end u=u(1:k,:); fprintf(欲保留%%%d的特征,最少需要保留%d个特征\n,thr*100,k); %保存K个含有主成分的特征向量 save(feature_PCA,u);完整代码如下：
%PCA主成分分析 clear load(2-Class Problem.mat); load(Mult-class Problem.mat); tic % 因为PCA分析时不需要标签信息，所以我们可以使用所有数据进行PCA，提高分析性能 datas=[Training_class1,Training_class2,Testing,Training_data,Testing_data];%将所有数据整合到一起 [d,n]=size(datas);%获取数据大小，d为维度，n为数据数量 % 去均值化 datas_mean=mean(datas,2); datas=datas-datas_mean; % 计算协方差阵 c=datas*datas/n; % 计算特征值和特征向量 [u,lamda]=eig(c); lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量 %将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列 lamda_u=[lamda;u]; lamda_u=lamda_u; % 对特征向量按lamda大小进行降序排列，并确定K，阈值选0.9 thr=0.9; lamda_u=sortrows(lamda_u,1,descend);%对特征向量按lamda大小进行降序排列 lamda=lamda_u(:,1);%分离特征值 u=lamda_u(:,2:end);%分离特征向量 %确定K值 for i=1:d res=sum(lamda(1:i))/sum(lamda); if res>thr k=i; break end end u=u(1:k,:); fprintf(欲保留%%%d的特征,最少需要保留%d个特征\n,thr*100,k); %保存K个含有主成分的特征向量 save(feature_PCA,u); toc程序运行结果分析：
可以看到最终维数越减到了2维，却保留了90%的信息量。
首先需要将原始数据进行去均值化，然后使用PCA分析得到的特征变换矩阵对维数进行约减，最后使用bayes分类器测试PCA效果，使用的数据集与之前遗传算法、SFS的测试数据集相同。 具体代码实现如下； （1）读取数据集
%PCA主成分分析性能测试–二分类,学习算法采用贝叶斯 clear load(2-Class Problem.mat); load(feature_PCA) tic n1=size(Training_class1,2); n2=size(Training_class2,2);（2）原始数据去均值化
%训练数据去均值化 Training=[Training_class1,Training_class2]; datas_mean=mean(Training,2); Training=Training-datas_mean; Training_class1=Training(:,1:n1); Training_class2=Training(:,n1+1:end); % 测试数据去均值化 datas_mean=mean(Testing,2); Testing=Testing-datas_mean;（3）进行维数约减
% 提取数据主成分,维数约减 Training_class1_b=u*Training_class1; Training_class2_b=u*Training_class2; Testing_b=u*Testing;（4）使用bayes分类器进行分类，测试PCA效果
% 先验概率 pw1=n1/(n1+n2); pw2=n2/(n1+n2); [miu1,sigma1]=ParamerEstimation(Training_class1_b); [miu2,sigma2]=ParamerEstimation(Training_class2_b); predict_label=0; [b,n]=size(Testing_b); for i=1:n x=Testing_b(:,i); pxw1=gaussian(miu1,sigma1,x); pxw2=gaussian(miu2,sigma2,x); if pw1*pxw1>pw2*pxw2 predict_label(i)=1; else predict_label(i)=2; end end % 计算精度 acc=sum(predict_label==Label_Testing)/n; toc fprintf(正确率是%.2f%%\n,acc*100);完整代码如下：
%PCA主成分分析性能测试–二分类,学习算法采用贝叶斯 clear load(2-Class Problem.mat); load(feature_PCA) tic n1=size(Training_class1,2); n2=size(Training_class2,2); %训练数据去均值化 Training=[Training_class1,Training_class2]; datas_mean=mean(Training,2); Training=Training-datas_mean; Training_class1=Training(:,1:n1); Training_class2=Training(:,n1+1:end); % 测试数据去均值化 datas_mean=mean(Testing,2); Testing=Testing-datas_mean; % 提取数据主成分,维数约减 Training_class1_b=u*Training_class1; Training_class2_b=u*Training_class2; Testing_b=u*Testing; % 先验概率 pw1=n1/(n1+n2); pw2=n2/(n1+n2); [miu1,sigma1]=ParamerEstimation(Training_class1_b); [miu2,sigma2]=ParamerEstimation(Training_class2_b); predict_label=0; [b,n]=size(Testing_b); for i=1:n x=Testing_b(:,i); pxw1=gaussian(miu1,sigma1,x); pxw2=gaussian(miu2,sigma2,x); if pw1*pxw1>pw2*pxw2 predict_label(i)=1; else predict_label(i)=2; end end % 计算精度 acc=sum(predict_label==Label_Testing)/n; toc fprintf(正确率是%.2f%%\n,acc*100);程序运行结果分析： 由此可见，对于二分类，想要正确分类，2维的数据就足够了。
五、多分类测试和二分类类似，需要注意的是，在进行测试之前，需要将原始数据去均值化。测试数据集同样使用之前遗传算法和SFS相同的测试数据。 完整代码如下：
%PCA主成分分析性能测试–多分类,学习算法采用贝叶斯 clear load(Mult-class Problem.mat); load(feature_PCA) tic %训练数据去均值化 datas_mean=mean(Training_data,2); Training_data=Training_data-datas_mean; % 测试数据去均值化 datas_mean=mean(Testing_data,2); Testing_data=Testing_data-datas_mean; % 提取数据主成分 Training_data=u*Training_data; Testing_data=u*Testing_data; % 获取类别数 class_nums=Label_training(end); test_nums=size(Testing_data,2); train_nums=size(Training_data,2); Training_temp=0; predict=0; for class=1:class_nums [miu(:,class),sigma(:,:,class)]=ParamerEstimation(Training_data(:,Label_training==class)); num=size(Training_data(:,Label_training==class),2); pw(class)=num/train_nums; end for i=1:test_nums for class=1:class_nums pxw(class)=gaussian(miu(:,class),sigma(:,:,class),Testing_data(:,i)); g_x(class)=log(pw(class))+log(pxw(class)); end [~,argmax]=max(g_x); predict(i)=argmax; if mod(i,100) == 0 acc=sum(predict==Label_testing(1:i))/(i); disp([预测数据号： num2str(i)]) disp([准确度是： num2str(acc)]) end end acc=sum(predict==Label_testing)/(test_nums); toc disp([总准确度是： num2str(acc)])测试结果；
使用PCA降维后，只用2维数据就能够达到多分类55%的正确率，时间只用了2.8s。
这篇文章为大家介绍了一种特征提取的方法——PCA方法，在进行PCA时，我们没有使用任何标签信息，即我们只是使用数据自身之间的差距进行降维，这对于分类任务可能不是非常友好，这样做的一个好处是我们可以利用所有数据，包括测试集和训练集，包括不同的分类任务，只要是相关数据，我们都可以用来进行PCA的降维，这样做的好处就是我们可以尽可能多的使用数据进行降维，但是这样的不足就是我们在进行降维时，不会考虑到我们具体的分类标准，这样我们无法针对具体的分类任务进行降维。下篇文章，我们将介绍一种会考虑到分类标签的特征提取方法，我们拭目以待
