之前的文章中，我们已经介绍了PCA，它在进行数据降维时，不考虑分类的情况，是利用数据自身进行特征提取的一种方法。这就使得PCA经常用于数据的降燥而不是数据的分类任务中。本篇文章要介绍的LDA方法，在进行特征提取时，将学习数据的标签信息也考虑在内，使得分类时的准确率大大增加。
LDA（Linear Discriminant Analysis），即线性判别分析。它的基本原理可以用一句话概括：将数据投影变换，使得相同类别数据之间的距离最小，不同类别数据之间的距离最大，简称：类间距离最大，类内距离最小。我们可以用一张图进行解释：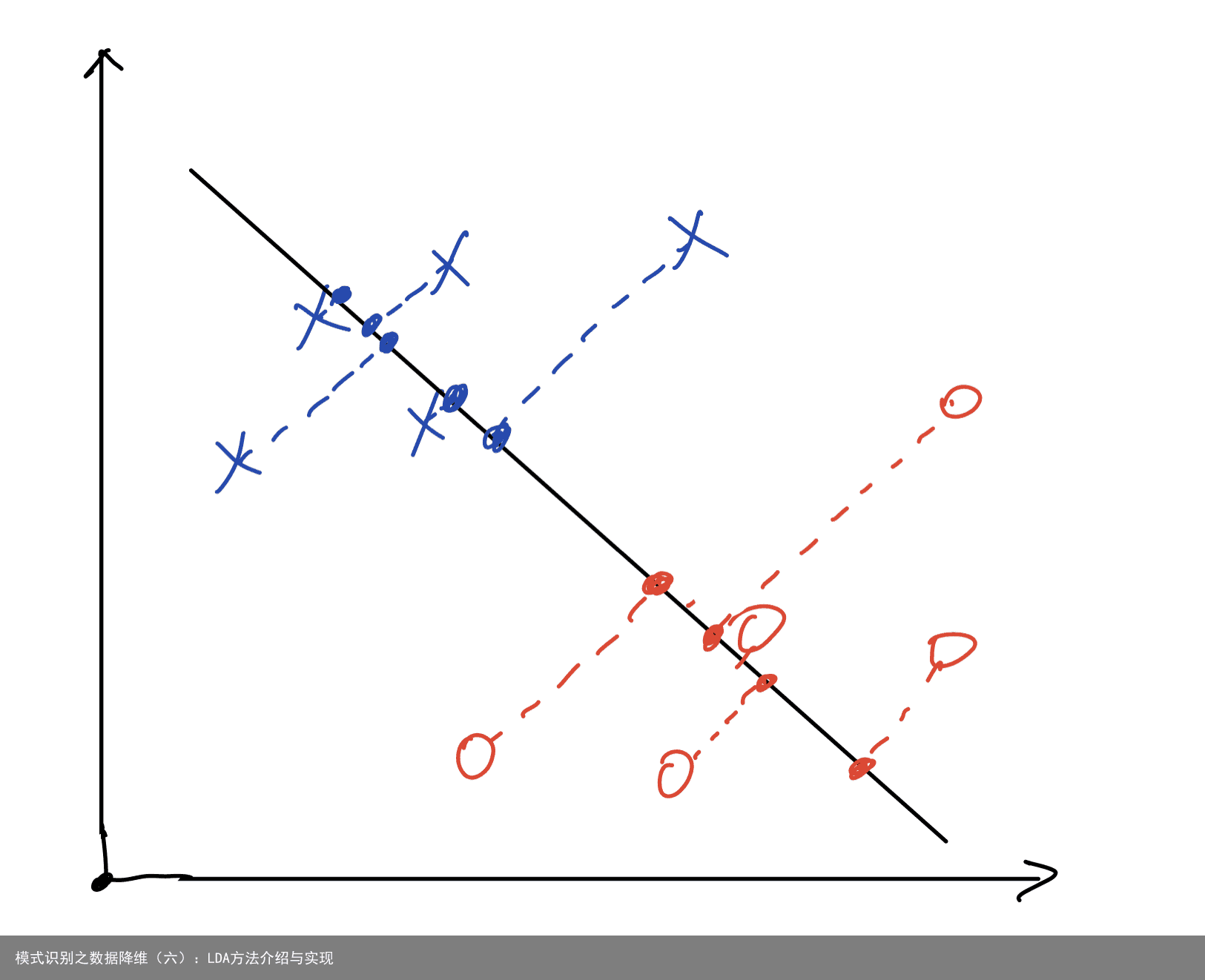
这张图大家已经很熟悉了，我们可以把蓝色的“X”和红色的“O”看作两类数据，在投影之后，我们可以看出，相同类别之间的距离很小，不同类别之间的距离很大。以上就是LDA的基本思想。那么这个类间距离和类内距离如何表示呢？数学家们已经为我们提供了相关公式了，如下所示：
（1）类内距离公式：
其中，C为类别个数，比如：二分类任务时，C=2.，xij为第i类的第j个数据，ui为第i类样本的均值。
（2）类间距离公式：
其中，ui为第i类样本的均值，u的计算公式如下：
我们最终的目的，就是要让类间距离最小，类内距离最大，我们可以设定一个判别式：
判别式最大时，我们的LDA达到最优
与PCA分析不同的是，LDA分析用到了数据的标签信息。所以，在进行二分类和多分类的降维操作时，要分开处理。在处理二分类数据时，最大的投影维度为1维。在处理多分类数据时，最大的投影维度为C-1维。 （1）先导入二分类数据，计算均值和内类离散度矩阵
%LDA clear % 先使用二分类数据进行LDA load(2-Class Problem.mat); tic train_num1=size(Training_class1,2); train_num2=size(Training_class2,2); d=size(Training_class1,1); % 计算均值 miu_1=mean(Training_class1,2); miu_2=mean(Training_class2,2); miu=(miu_1+miu_2)/2; % 计算类内离散度矩阵 s_w1=(Training_class1-miu_1)*(Training_class1-miu_1); s_w2=(Training_class2-miu_2)*(Training_class2-miu_2); s_w=s_w1+s_w2;（2）计算类间离散度矩阵，的特征值以及特征向量。并对特征值进行排列
% 计算类间离散度矩阵 s_b=(miu_1-miu_2)*(miu_1-miu_2); % 计算特征值和特征向量 [u,lamda]=eig(s_w\s_b); lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量 % 将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列 lamda_u=[lamda;u]; lamda_u=lamda_u; lamda_u=sortrows(lamda_u,1,descend);%对特征向量按lamda大小进行降序排列 lamda=lamda_u(:,1);%分离特征值 u=lamda_u(:,2:end);%分离特征向量（3）求解变换矩阵，并保存
k=1;%提取的特征数为1,对于二分类问题，最大的投影维度为1维 u=u(1:k,:); u_2_class=u; %保存提取的特征向量 save(feature_LDA,u_2_class);（4）读取多分类数据集
% 使用多分类数据进行LDA load(Mult-class Problem.mat); % 获取类别数 class_nums=Label_training(end); % 训练数据量 train_num=size(Training_data,2);（5）计算均值、类内离散度矩阵
% 计算均值、类内离散度矩阵 for i=1:class_nums miu_i(:,i)=mean(Training_data(:,Label_training==i),2);%均值 %第i类类内离散度矩阵 s=0; for j=1:train_num s=s+(Training_data(:,Label_training==i)-miu_i(:,i))*(Training_data(:,Label_training==i)-miu_i(:,i)); end s_w_i(:,:,i)=s; end miu=mean(miu_i,2); s_w=sum(s_w_i,3);（6）计算类间离散度矩阵，的特征值以及特征矩阵，并对特征向量，并对特征向量按特征值降序排列。
% 计算类间离散度 s_b=(miu_i-miu)*(miu_i-miu); % 计算特征值和特征向量 [u,lamda]=eig(inv(s_w)*s_b); lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量 %将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列 lamda_u=[lamda;u]; lamda_u=lamda_u; lamda_u=sortrows(lamda_u,1,descend);%对特征向量按lamda大小进行降序排列 lamda=lamda_u(:,1);%分离特征值 u=lamda_u(:,2:end);%分离特征向量（7）计算变换矩阵，并保存
k=16;%提取的最大特征数为c-1=16 u=u(1:k,:); u_mult_class=u; %保存提取的特征向量 save(feature_LDA,u_mult_class,-append); toc完整代码如下：
%LDA clear % 先使用二分类数据进行LDA load(2-Class Problem.mat); tic train_num1=size(Training_class1,2); train_num2=size(Training_class2,2); d=size(Training_class1,1); % 计算均值 miu_1=mean(Training_class1,2); miu_2=mean(Training_class2,2); miu=(miu_1+miu_2)/2; % 计算类内离散度矩阵 s_w1=(Training_class1-miu_1)*(Training_class1-miu_1); s_w2=(Training_class2-miu_2)*(Training_class2-miu_2); s_w=s_w1+s_w2; % 计算类间离散度矩阵 s_b=(miu_1-miu_2)*(miu_1-miu_2); % 计算特征值和特征向量 [u,lamda]=eig(s_w\s_b); lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量 % 将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列 lamda_u=[lamda;u]; lamda_u=lamda_u; lamda_u=sortrows(lamda_u,1,descend);%对特征向量按lamda大小进行降序排列 lamda=lamda_u(:,1);%分离特征值 u=lamda_u(:,2:end);%分离特征向量 k=1;%提取的特征数为1,对于二分类问题，最大的投影维度为1维 u=u(1:k,:); u_2_class=u; %保存提取的特征向量 save(feature_LDA,u_2_class); % 使用多分类数据进行LDA load(Mult-class Problem.mat); % 获取类别数 class_nums=Label_training(end); % 训练数据量 train_num=size(Training_data,2); % 计算均值、类内离散度矩阵 for i=1:class_nums miu_i(:,i)=mean(Training_data(:,Label_training==i),2);%均值 %第i类类内离散度矩阵 s=0; for j=1:train_num s=s+(Training_data(:,Label_training==i)-miu_i(:,i))*(Training_data(:,Label_training==i)-miu_i(:,i)); end s_w_i(:,:,i)=s; end miu=mean(miu_i,2); s_w=sum(s_w_i,3); % 计算类间离散度 s_b=(miu_i-miu)*(miu_i-miu); % 计算特征值和特征向量 [u,lamda]=eig(inv(s_w)*s_b); lamda=ones(1,d)*lamda;%eig函数生成的特征值转换成行向量 %将特征值和特征向量合成一个矩阵，第一列为特征值，从第二列开始为特征向量，特征向量按行排列 lamda_u=[lamda;u]; lamda_u=lamda_u; lamda_u=sortrows(lamda_u,1,descend);%对特征向量按lamda大小进行降序排列 lamda=lamda_u(:,1);%分离特征值 u=lamda_u(:,2:end);%分离特征向量 k=16;%提取的最大特征数为c-1=16 u=u(1:k,:); u_mult_class=u; %保存提取的特征向量 save(feature_LDA,u_mult_class,-append); toc程序运行结果：
四、LDA的二分类测试下面，我们将测试使用LDA降维后的数据的分类效果。二分类测试数据和测试算法与PCA及以前的测试相同。先对数据利用LDA生成的变换矩阵进行降维，然后使用贝叶斯算法进行分类，观察正确率和程序运行时间。 完整代码如下：
%LDA性能测试–二分类,学习算法采用贝叶斯 clear load(2-Class Problem.mat); load(feature_LDA) tic n1=size(Training_class1,2); n2=size(Training_class2,2); % 特征提取 Training_class1_b=u_2_class*Training_class1; Training_class2_b=u_2_class*Training_class2; Testing_b=u_2_class*Testing; % 先验概率 pw1=n1/(n1+n2); pw2=n2/(n1+n2); [miu1,sigma1]=ParamerEstimation(Training_class1_b); [miu2,sigma2]=ParamerEstimation(Training_class2_b); predict_label=0; [b,n]=size(Testing_b); for i=1:n x=Testing_b(:,i); pxw1=gaussian(miu1,sigma1,x); pxw2=gaussian(miu2,sigma2,x); if pw1*pxw1>pw2*pxw2 predict_label(i)=1; else predict_label(i)=2; end end % 计算精度 acc=sum(predict_label==Label_Testing)/n; toc fprintf(正确率是%.2f%%\n,acc*100);程序运行结果： 二分类最终降到一维，也可以达到100%的正确分类，时间只用了0.01s
五、多分类测试同二分类，先进行降维，然后进行贝叶斯多分类。使用的数据集也与之前的算法测试数据集一致 完整代码如下：
%PCA主成分分析性能测试–多分类,学习算法采用贝叶斯 clear load(Mult-class Problem.mat); load(feature_LDA) tic % 特征提取 u=u_mult_class; Training_data=u*Training_data; Testing_data=u*Testing_data; % 获取类别数 class_nums=Label_training(end); % 获取数据集大小 test_nums=size(Testing_data,2); train_nums=size(Training_data,2); Training_temp=0; predict=0; for class=1:class_nums [miu(:,class),sigma(:,:,class)]=ParamerEstimation(Training_data(:,Label_training==class)); num=size(Training_data(:,Label_training==class),2); % 计算先验概率 pw(class)=num/train_nums; end for i=1:test_nums for class=1:class_nums % 计算类的条件概率 pxw(class)=gaussian(miu(:,class),sigma(:,:,class),Testing_data(:,i)); % 计算判别式 g_x(class)=log(pw(class))+log(pxw(class)); end [~,argmax]=max(g_x); predict(i)=argmax; if mod(i,100) == 0 acc=sum(predict==Label_testing(1:i))/(i); disp([预测数据号： num2str(i)]) disp([准确度是： num2str(acc)]) end end % 计算正确率 acc=sum(predict==Label_testing)/(test_nums); toc disp([总准确度是： num2str(acc)])程序运行结果：
可以看到，由于使用了类别的标签信息，LDA降维后可以达到70%的正确率。况且只用了7s左右。
本篇文章介绍了LDA特征提取的方法和实现，并进行了二分类和多分类的测试，并与PCA进行了对比，LDA掩饰了PCA算法的不做，最终效果十分不错。至此，所有关于数据降维的内容已经介绍完毕。
