机器学习（二）：使用线性回归模型进行房价预测

  之前，我们介绍了关于回归的相关内容，并成功地拟合出一条直线。本篇文章我们将使用回归模型进行房价预测。本次我们的预测任务是：根据房屋面积对房价进行预测。这是一个一元回归任务，较为简单。下面我们一起来看一下回归模型在房价预测上的表现。

一、数据集介绍

  如图：该数据集以行为单位，第一列为房屋的面积，第二列为房屋的价格，一共870条数据。 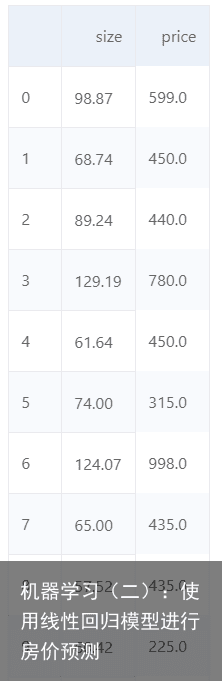  我们将数据集划分为600条训练集和270条测试集。首先在训练集上进行训练，拟合出关系式，然后用这个关系式对测试集的数据进行测试。下面我们介绍一下数据处理部分的编程实现：

  利用pandas库导入数据集：

import pandas as pd import numpy as np datasFile=pd.read_csv(data/data1810/data.txt,names=[size,price]) datas=np.array(datasFile)

  划分数据集：

import matplotlib.pyplot as plt # 划分数据集为训练集和测试集 trainSet=datas[0:600,:] testSet=datas[600:,:] trainX=trainSet[:,0] trainY=trainSet[:,1] testX=testSet[:,0] testY=testSet[:,1]

  归一化数据集。数据的归一化是数据分析的一种常用手段，一方面，将所有数据按比例划分至同一范围，可以增加不同类型数据之间的可比性，另一方面，若数据量值过大，则算法会发生振荡，不好收敛；若数据量过小，则会降低算法收敛速度，因此需要将数据等比例划分至同一范围，即归一化处理。本文我们按照以下公式归一化数据： 代码如下：

# 归一化数据，最大最小值按照训练数据集来取 trainX_min_max=(trainX-np.min(trainX))/(np.max(trainX)-np.min(trainX)); trainY_min_max=(trainY-np.min(trainY))/(np.max(trainY)-np.min(trainY)); testX_min_max=(testX-np.min(testX))/(np.max(testX)-np.min(testX)); testY_min_max=(testY-np.min(testY))/(np.max(testY)-np.min(testY));

  将归一化后的数据绘制到二维平面，横轴为房屋面积，纵轴为价格。相关代码如下：

plt.subplot(1,2,1) plt.scatter(trainX_min_max,trainY_min_max) plt.subplot(1,2,2) plt.scatter(testX_min_max,testY_min_max)

绘制出来的图像如下：（左图为训练数据，右图为测试数据）

二、使用线性回归进行房屋预测

  按照之前文章中介绍的基于梯度下降法的线性回归模型，我们首先对归一化后的数据进行训练。需要注意的是，我们在训练之前会随机产生两组数作为参数a，b的初始化方法，这样能够防止算法总是收敛至局部最优点，虽然在线性回归模型中，损失函数只有一个极小值，不存在局部最优的情况，但其他的模型中，我们会经常用到此方法来初始化我们的训练模型。训练数据的代码部分如下：

import random # 初始化回归相关参数值 a=random.random()# 随机初始化一个值 b=random.random() x=trainX_min_max y=trainY_min_max lr=0.05# 学习率 iter=1000 # 训练次数 # 开始训练 for i in range(iter): predict=a*x+b # 使用线性函数预测 # 计算损失函数 J=np.mean((predict-y)*(predict-y)) # 计算损失函数的梯度值 J_grad_a=np.mean((predict-y)*x) J_grad_b=np.mean(predict-y) # 进行参数迭代 a=a-lr*J_grad_a b=b-lr*J_grad_b # 打印参数的值 print(“iter=%d,” % i) print(“cost=%.3f” % J) print(“a=%.3f,” % a) print(“b=%.3f,” % b) print(“\n”)

最终结果如下： 可以看到，算法最终收敛，训练集的误差为0.008   我们将线性回归模型拟合出的直线与训练集数据绘制在一起进行对比，发现模型能够很好地贴合数据的走向。相关代码如下：

plt.scatter(trainX_min_max,trainY_min_max) plt.plot(x,predict)

结果如下：   使用训练好的模型进行预测，并计算误差，然后如同训练部分绘制拟合出的直线与测试数据的对比图。：

# 进行预测 x=testX_min_max y=testY_min_max result=a*x+b # 计算预测误差 err=np.mean((result-y)*(result-y)) # 打印误差 print(err=%.3f % err) # 绘制拟合结果 plt.scatter(x,y) plt.plot(x,result)

运行结果如下： 我们发现预测误差为0.018，绘制的结果也能够看出来，拟合出的直线能较好地贴合数据。 完整代码如下：

import pandas as pd import numpy as np datasFile=pd.read_csv(data/data1810/data.txt,names=[size,price]) datas=np.array(datasFile) import matplotlib.pyplot as plt trainSet=datas[0:600,:] testSet=datas[600:,:] trainX=trainSet[:,0] trainY=trainSet[:,1] testX=testSet[:,0] testY=testSet[:,1] # 归一化数据，最大最小值按照训练数据集来取 trainX_min_max=(trainX-np.min(trainX))/(np.max(trainX)-np.min(trainX)); trainY_min_max=(trainY-np.min(trainY))/(np.max(trainY)-np.min(trainY)); testX_min_max=(testX-np.min(testX))/(np.max(testX)-np.min(testX)); testY_min_max=(testY-np.min(testY))/(np.max(testY)-np.min(testY)); plt.subplot(1,2,1) plt.scatter(trainX_min_max,trainY_min_max) plt.subplot(1,2,2) plt.scatter(testX_min_max,testY_min_max) import random # 初始化回归相关参数值 a=random.random()# 随机初始化一个值 b=random.random() x=trainX_min_max y=trainY_min_max lr=0.05# 学习率 iter=1000 # 训练次数 # 开始训练 for i in range(iter): predict=a*x+b # 使用线性函数预测 # 计算损失函数 J=np.mean((predict-y)*(predict-y)) # 计算损失函数的梯度值 J_grad_a=np.mean((predict-y)*x) J_grad_b=np.mean(predict-y) # 进行参数迭代 a=a-lr*J_grad_a b=b-lr*J_grad_b # 打印参数的值 print(“iter=%d,” % i) print(“cost=%.3f” % J) print(“a=%.3f,” % a) print(“b=%.3f,” % b) print(“\n”) plt.scatter(trainX_min_max,trainY_min_max) plt.plot(x,predict) # 进行预测 x=testX_min_max y=testY_min_max result=a*x+b # 计算预测误差 err=np.mean((result-y)*(result-y)) # 打印误差 print(err=%.3f % err) # 绘制拟合结果 plt.scatter(x,y) plt.plot(x,result) 三、总结

  线性回归模型是最简单的回归模型，我们能够看出来，这个模型并不能很好的贴合数据，但能基本预测数据的走向。若想要更好地贴合数据，我们就需要采用更复杂的回归模型。然而，复杂的模型带来的是更长的耗时，除此之外，还会带来其他的问题，这些在之后的文章中会进行介绍。