【深度学习】深度神经网络框架的探索(从Regression说起)

1 从逻辑回归说起 2 深度学习框架 3 基于反向传播算法的自动求导 4 简单深度神经网络框架实现 4.1 数据结构 4.2 计算图组件 4.3 训练模型（部分代码） 1 从逻辑回归说起

神经网络可以用来模拟回归问题 (regression)，例如给下面一组数据，用一条线来对数据进行拟合，并可以预测新输入 x 的输出值。 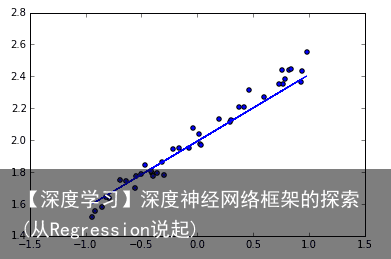导入模块并创建数据 models.Sequential，用来一层一层一层的去建立神经层； layers.Dense 意思是这个神经层是全连接层。

建立模型 然后用 Sequential 建立 model， 再用 model.add 添加神经层，添加的是 Dense 全连接神经层。

参数有两个，一个是输入数据和输出数据的维度，本代码的例子中 x 和 y 是一维的。

如果需要添加下一个神经层的时候，不用再定义输入的纬度，因为它默认就把前一层的输出作为当前层的输入。在这个例子里，只需要一层就够了。

model = Sequential() model.add(Dense(output_dim=1, input_dim=1))

激活模型 接下来要激活神经网络，上一步只是定义模型。

参数中，误差函数用的是 mse 均方误差；优化器用的是 sgd 随机梯度下降法。

choose loss function and optimizing method

model.compile(loss=mse, optimizer=sgd) 以上三行就构建好了一个神经网络，它比 Tensorflow 要少了很多代码，很简单。

可视化结果 最后可以画出预测结果，与测试集的值进行对比。

plotting the prediction

Y_pred = model.predict(X_test) plt.scatter(X_test, Y_test) plt.plot(X_test, Y_pred) plt.show()

2 深度学习框架

近几年最火的深度学习框架是什么?毫无疑问，TensorFlow 高票当选。同时Caffe、PyTorch、MXNet、CNTK用得也非常多。这些框架虽各有优势，但都具有一些普遍特征，据Gokula Krishnan Santhanam总结，大部分深度学习框架都包含以下五个核心组件:

(1)张量(Tensor) 的数据结构。 (2)基于张量的各种操作。 (3) (Computation Graph) (4) (Automatic Differentiation) (5) BLAS cuBLAS. cuDNN 4 tiRE.

其中，张量(Tensor)可以理解为任意维度的数组一-比 如一维数组被称作向量(Vector) ，三维的被称作矩阵(Matrix) ，这些都属于张量。有了张量，就有对应的基本操作，如取某行某列的值、张量乘以常数等。运用拓展包其实就相当于使用底层计算软件加速运算。我们今天重点介绍的就是计算图模型和自动微分两部分。首先谈谈如何实现自动求导，然后用最简单的方法实现这两部分。

3 基于反向传播算法的自动求导

首先看正向传播。给定函数e= (a+ b)(b+1)，当a=2、b=1时，进行正向传播，其实就是小学乘法，即将a=2、 b=1带入，e=(a+b)(b+ 1)=3×2=6。反向传播过程就麻烦一-些了.我们暂日可以将这个式子直接运用求导法则进行求导。

自动微分（Automatic Differentiation，简称AD）也称自动求导，算法能够计算可导函数在某点处的导数值的计算，是反向传播算法的一般化。自动微分要解决的核心问题是计算复杂函数，通常是多层复合函数在某一点处的导数，梯度，以及Hessian矩阵值。它对用户屏蔽了繁琐的求导细节和过程。目前知名的深度学习开源库均提供了自动微分的功能，包括TensorFlow、pytorch等。

对于编程计算目标函数的导数值，目前有4种方法：手动微分，数值微分，符号微分，以及自动微分，在接下来会分别进行介绍。

自动微分在深度学习库中的地位

自动微分技术在深度学习库中处于重要地位，是整个训练算法的核心组件之一。一个典型的深度学习库架构如下图所示。在这里忽略了网络通信，本地IO等模块。

梯度计算一般使用本文所讲述的自动微分技术，计算出梯度值给优化器使用，用于训练阶段。如果使用标准的梯度下降法进行迭代，在第k次迭代时的计算公式为

可以理解为看你和真实值差多少而已，然后反向传播，不断调整。

4 简单深度神经网络框架实现

4.1 数据结构

class Node(object): “”” Base class for nodes in the network. Arguments: `inbound_nodes`: A list of nodes with edges into this node. “”” def __init__(self, inbound_nodes=[]): “”” Nodes constructor (runs when the object is instantiated). Sets properties that all nodes need. “”” # A list of nodes with edges into this node. self.inbound_nodes = inbound_nodes # The eventual value of this node. Set by running # the forward() method. self.value = None # A list of nodes that this node outputs to. self.outbound_nodes = [] # New property! Keys are the inputs to this node and # their values are the partials of this node with # respect to that input. self.gradients = {} # Sets this node as an outbound node for all of # this nodes inputs. for node in inbound_nodes: node.outbound_nodes.append(self) def forward(self): “”” Every node that uses this class as a base class will need to define its own `forward` method. “”” raise NotImplementedError def backward(self): “”” Every node that uses this class as a base class will need to define its own `backward` method. “”” raise NotImplementedError class Input(Node): “”” A generic input into the network. “”” def __init__(self): Node.__init__(self) def forward(self): pass def backward(self): self.gradients = {self: 0} for n in self.outbound_nodes: self.gradients[self] += n.gradients[self] class Linear(Node): “”” Represents a node that performs a linear transform. “”” def __init__(self, X, W, b): Node.__init__(self, [X, W, b]) def forward(self): “”” Performs the math behind a linear transform. “”” X = self.inbound_nodes[0].value W = self.inbound_nodes[1].value b = self.inbound_nodes[2].value self.value = np.dot(X, W) + b def backward(self): “”” Calculates the gradient based on the output values. “”” self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes} for n in self.outbound_nodes: grad_cost = n.gradients[self] self.gradients[self.inbound_nodes[0]] += np.dot(grad_cost, self.inbound_nodes[1].value.T) self.gradients[self.inbound_nodes[1]] += np.dot(self.inbound_nodes[0].value.T, grad_cost) self.gradients[self.inbound_nodes[2]] += np.sum(grad_cost, axis=0, keepdims=False) class Sigmoid(Node): “”” Represents a node that performs the sigmoid activation function. “”” def __init__(self, node): Node.__init__(self, [node]) def _sigmoid(self, x): “”” This method is separate from `forward` because it will be used with `backward` as well. `x`: A numpy array-like object. “”” return 1. / (1. + np.exp(-x)) def forward(self): “”” Perform the sigmoid function and set the value. “”” input_value = self.inbound_nodes[0].value self.value = self._sigmoid(input_value) def backward(self): “”” Calculates the gradient using the derivative of the sigmoid function. “”” self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes} for n in self.outbound_nodes: grad_cost = n.gradients[self] sigmoid = self.value self.gradients[self.inbound_nodes[0]] += sigmoid * (1 – sigmoid) * grad_cost class MSE(Node): def __init__(self, y, a): “”” The mean squared error cost function. Should be used as the last node for a network. “”” Node.__init__(self, [y, a]) def forward(self): “”” Calculates the mean squared error. “”” y = self.inbound_nodes[0].value.reshape(-1, 1) a = self.inbound_nodes[1].value.reshape(-1, 1) self.m = self.inbound_nodes[0].value.shape[0] self.diff = y – a self.value = np.mean(self.diff**2) def backward(self): “”” Calculates the gradient of the cost. “”” self.gradients[self.inbound_nodes[0]] = (2 / self.m) * self.diff self.gradients[self.inbound_nodes[1]] = (-2 / self.m) * self.diff

4.2 计算图组件

源深度学习库Tensorflow通过计算图（Computational Graph）表述计算流程。学过数据结构的同学都不会对图的概念陌生。Tensorflow中的每一个数据都是计算图上的一个节点，节点之间的边描述了数据之间的计算即流向关系。下面是一个典型的计算图。

该图所表示的运算为

其中节点 v1，v2为表示中间结果或最终结果的变量。在后面的讲述中，将会以计算图作为工具。

# python def topological_sort(feed_dict): “”” Sort the nodes in topological order using Kahns Algorithm. `feed_dict`: A dictionary where the key is a `Input` Node and the value is the respective value feed to that Node. Returns a list of sorted nodes. “”” input_nodes = [n for n in feed_dict.keys()] G = {} nodes = [n for n in input_nodes] while len(nodes) > 0: n = nodes.pop(0) if n not in G: G[n] = {in: set(), out: set()} for m in n.outbound_nodes: if m not in G: G[m] = {in: set(), out: set()} G[n][out].add(m) G[m][in].add(n) nodes.append(m) L = [] S = set(input_nodes) while len(S) > 0: n = S.pop() if isinstance(n, Input): n.value = feed_dict[n] L.append(n) for m in n.outbound_nodes: G[n][out].remove(m) G[m][in].remove(n) if len(G[m][in]) == 0: S.add(m) return L

4.3 训练模型（部分代码）

一个优化例子： 再看代码：

# 随机初始化参数值 W1_0 = np.random.random(X_.shape[1]*n_hidden).reshape([X_.shape[1], n_hidden]) W2_0 = np.random.random(n_hidden*n_class).reshape([n_hidden, n_class]) b1_0 = np.random.random(n_hidden) b2_0 = np.random.random(n_class) # 将输入值带入算子 feed_dict = { X: X_, y: y_, W1: W1_0, b1: b1_0, W2: W2_0, b2: b2_0 } # 训练参数 # 这里训练100轮（eprochs），每轮抽4个样本（batch_size）训练150/4次（steps_per_eproch）,学习率 0.1 epochs = 100 m = X_.shape[0] batch_size = 4 steps_per_epoch = m // batch_size lr = 0.1 graph = topological_sort(feed_dict) trainables = [W1, b1, W2, b2] l_Mat_W1 = [W1_0] l_Mat_W2 = [W2_0] l_loss = [] for i in range(epochs): loss = 0 for j in range(steps_per_epoch): X_batch, y_batch = resample(X_, y_, n_samples=batch_size) X.value = X_batch y.value = y_batch forward_and_backward(graph) sgd_update(trainables, lr) loss += graph[-1].value l_loss.append(loss) if i % 10 == 9: print(“Eproch %d, Loss = %1.5f” % (i, loss))