行波进位/超前进位加法器详解-超前进位加法器和串行进位加法器

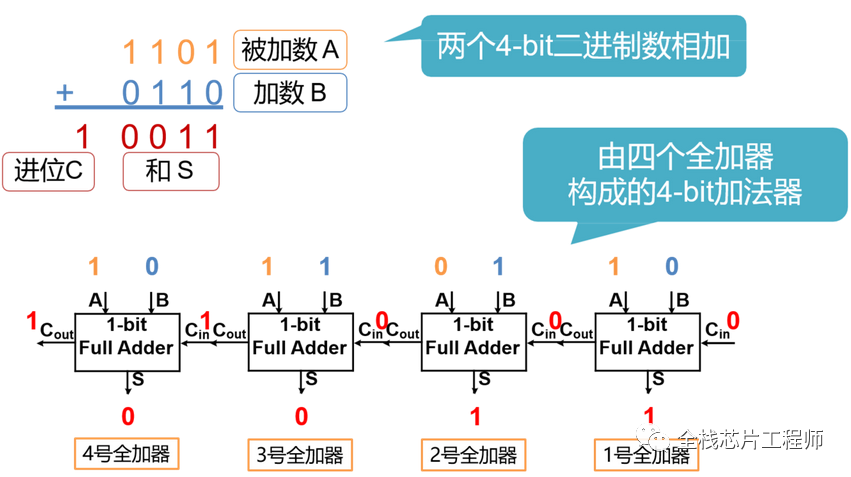
行波进位加法器是串行执行的，其高位的运算要依赖低位的进位，所以当输入数据的位数较多时，会形成很大的延迟并可能成为芯片的关键路径。

采用超前进位加法器（也叫先行进位加法器）可以有效减小这种延迟。下面介绍超前进位加法器的设计原理。设二进制加法器第i位为Ai，Bi，输出为Si，进位输入为Ci，进位输出为C(i+1)，则有：

Si=Ai⊕Bi⊕Ci；

C(i+1)=Ai*Bi+Ai*Ci+Bi*Ci=Ai*Bi+(Ai+Bi)*Ci;

令：Gi=Ai*Bi, Pi=Ai+Bi；

则有：

C(i+1)=Gi+Pi*Ci；

当 Ai 和 Bi 都为1时，Gi=1，产生进位C(i+1)=1；

当 Ai 和 Bi 有一个为1时，Pi=1，传递进位C(i+1)=Ci；

说明：“*”表示与逻辑、“+”表示或逻辑、“⊕”表示异或逻辑。将Gi定义为进位产生信号，Pi定义为进位传递信号，Gi的优先级比Pi高。当Gi=1时，此时也有 Pi=1，无条件的产生进位，不管Ci是多少；当Gi=0而Pi=1时，进位输出为Ci，跟Ci之前的逻辑有关；

4bits超前进位加法器设计

设4位加数和被加数为A和B，进位输入为C_in，进位输出为C_out，对于第i位的进位产生Gi=Ai*Bi，进位传递Pi=Ai+Bi，i=0,1,2,3。于是各级进位输出，递归的展开Ci，有：C0=Cin;C1=G0+P0·C0;C2=G1+P1·C1=G1+P1·(G0+P0·C0) = G1+P1·G0+P1·P0·C0;C3=G2+P2·C2=G2+P2·G1+P2·P1·G0+P2·P1·P0·C0;C4=G3+P3·C3=G3+P3·G2+P3·P2·G1+P3·P2·P1·G0+P3·P2·P1·P0·C0;Cout=C4;由此可以看出，各级进位并行产生、彼此独立，只与输入数据Ai、Bi和C_in有关，减小了串行进位产生的延迟。该电路的运算核心是超前进位部件（Carry Lookahead Unit），也称为CLA部件。

C0=Cin;C1=G0+P0·C0;C2=G1+P1·C1=G1+P1·(G0+P0·C0) = G1+P1·G0+P1·P0·C0;C3=G2+P2·C2=G2+P2·G1+P2·P1·G0+P2·P1·P0·C0;C4=G3+P3·C3=G3+P3·G2+P3·P2·G1+P3·P2·P1·G0+P3·P2·P1·P0·C0;Cout=C4;可以得到4bits超前进位加法器的CLA的等效Gm、Pm值：令C4=Gm+Pm·Cin，又因为：C4=G3+P3·C3=G3+P3·G2+P3·P2·G1+P3·P2·P1·G0+P3·P2·P1·P0·C0；Gm=G3+P3·G2+P3·P2·G1+P3·P2·P1·G0；Pm=P3·P2·P1·P0；

以此

类推，我们可以发现规律，2bit超前进位加法G、P值计算可以类推到4bit超前进位加法，4bit超前进位加法G、P值计算可以类推到16bit超前进位加法。比如2bit超前进位加法：

令C2=Gm+Pm·Cin，又因为：C2=G1+P1·C1=G1+P1·(G0+P0·C0) = G1+P1·G0+P1·P0·C0;Gm=G1+P1·G0；Pm=P1·P0；发现什么了吗？

由2bit超前进位加法的G、P值计算可以类推到4bit超前进位加法：

即，高2bit的G、P值和低2bit的G、P值计算分别如下：Gh=G3+P3·G2；Ph=P3·P2；Gl=G1+P1·G0；Pl=P1·P0；那么4bit超前进位加法的G、P值可类推出：G=Gh+Ph·Gl=(G3+P3·G2)+P3·P2(G1+P1·G0)=G3+P3·G2+P3·P2·G1+P3·P2·P1·G0;P=Ph·Pl=P3·P2·P1·P0；

显然与上文的计算结果一致，因此由2bit超前进位加法的G、P值计算可以类推到4bit超前进位加法。同样，由4bit超前进位加法的G、P值计算可以类推到16bit超前进位加法。

4bits超前进位加法器的CLA的参考逻辑设计如下：

那么16bits的超前进位加法器如何设计？可以采用4个超前进位加法器级联的办法，缺点是该方法是超前进位+行波进位的组合设计，进位逻辑并不是最快的，因为可以采用上文提到的由4bit超前进位加法的G、P值计算可以类推到16bit超前进位加法。

16bits超前进位加法器设计

同理，我们得到了4bits的超前进位加法器的Gm、Pm值后，可以例化4个4bits的超前进位加法器完成16bits超前进位加法器的设计，当然需要再次例化上图所示的CLA_4的模块，根据4个4bits的超前进位加法器的Gm、Pm值快速并行算出进位C16的值。